链接
比赛
题目
A
题意
一个人可能注册多个账号,一个人的主账号最多能对应 $2$ 个副账号。
副账号名与主账号名能配对当且仅当其最长公共子串之长等于主副账号长度的较小值。
给定 $n$ 个长度上限为 $10$ 的主账号名,$m$ 个长度上限为 $10$ 的副账号名。
问有多少种配对的情况。两种配对方案不同当且仅当存在某个副账号对应的主账号不同。
保证所有账号名均不相同。
$T\le 100,n,m\le 1000$。
题解
建出Trie树以后,配对关系变为祖先关系。
考虑Trie上进行树形DP,设 $f_{u,a,b}$ 表示考虑到子树 $u$ 的时候,子树中有 $a$ 个主账号要与上面的匹配,有 $b$ 个副账号要与上面的主账号匹配的方案数。答案显然为 $f_{root,0,0}$。
显然当 $a\le 10,b\le 20$ 时,$f$ 值才有意义。
考虑 $f$ 的转移,相当于是一个二维的树形背包,然后合并完子树后再单独考虑根节点的贡献。
由于树形背包的性质,时间复杂度 $O(T\times 10\times 10\times 20\times (n+m))$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const ll mod=1e9+7;
inline ll Add(ll x,ll y){x+=y; return (x<mod)?x:x-mod;}
inline ll Dec(ll x,ll y){x-=y; return (x<0)?x+mod:x;}
inline void ADD(int &x,int y){x+=y; (x<mod)?0:x-=mod;}
inline ll Mul(ll x,ll y){return x*y%mod;}
inline ll Pow(ll x,ll y)
{
y%=(mod-1);ll ans=1;for(;y;y>>=1,x=x*x%mod)if(y&1) ans=ans*x%mod;
return ans;
}
const int N=20000;
const int S=26;
const int M=21;
int ne[N][S];
int f[N][M][M],g[M][M],tp[N],siz;
void init()
{
fo(i,1,siz)
{
fo(j,0,25) ne[i][j]=0;
tp[i]=0;
}
siz=1;
}
inline void ins(char *s,int opt)
{
int n=strlen(s+1),u=1,c;
fo(i,1,n)
{
c=s[i]-'a';
if(!ne[u][c]) ne[u][c]=++siz;
u=ne[u][c];
}
tp[u]=opt;
}
void dfs(int u)
{
fo(a,0,10) fo(b,0,20) f[u][a][b]=0;
f[u][0][0]=1;
fo(t,0,25)
if(ne[u][t])
{
int v=ne[u][t];
dfs(v);
fo(a,0,10)
fo(b,0,20)
if(f[u][a][b])
fo(c,0,10-a)
fo(d,0,20-b)
if(f[v][c][d])
ADD(g[a+c][b+d],Mul(f[u][a][b],f[v][c][d]));
fo(a,0,10) fo(b,0,20) f[u][a][b]=g[a][b],g[a][b]=0;
}
if(tp[u]==1)
{
fo(a,0,10)
fo(b,0,20)
if(f[u][a][b])
{
ADD(g[a][b],f[u][a][b]);
if(a<=9) ADD(g[a+1][b],f[u][a][b]);
if(a<=8) ADD(g[a+2][b],Mul((mod+1)>>1,f[u][a][b]));
if(b>=1) ADD(g[a][b-1],Mul(b,f[u][a][b]));
if(b>=2) ADD(g[a][b-2],Mul(b*(b-1)/2,f[u][a][b]));
if(b>=1&&a<=9) ADD(g[a+1][b-1],Mul(b,f[u][a][b]));
}
fo(a,0,10)
fo(b,0,20)
f[u][a][b]=g[a][b],g[a][b]=0;
}
if(tp[u]==2)
{
fo(a,0,10)
fo(b,0,20)
if(f[u][a][b])
{
ADD(g[a][b],f[u][a][b]);
if(a>=1) ADD(g[a-1][b],Mul(a,f[u][a][b]));
if(b<=19) ADD(g[a][b+1],f[u][a][b]);
}
fo(a,0,10)
fo(b,0,20)
f[u][a][b]=g[a][b],g[a][b]=0;
}
}
inline int solve()
{
dfs(1);
return f[1][0][0];
}
char s[M];
int main()
{
int n,m;
CASET
{
printf("Case #%d: ",___);
n=read(); m=read();
init();
fo(i,1,n)
{
scanf("%s",s+1);
ins(s,1);
}
fo(i,1,m)
{
scanf("%s",s+1);
ins(s,2);
}
printf("%lld\n",solve());
}
return 0;
}
|
B
做过的题,竟然还能调这么久。
到最后发现是一个智障错误,也是十分无语。
每个随机变量中总有一个概率最大的,记这个最大的是 $a_i$,那么选到其他概率都不会超过 $\frac{1}{2}$。
题目要求的精度是 $10^{-9}$,那么进行 $30$ 多次之后就会变成 $0$,也就是失配不会超过 $30$ 次。
发现时间卡得有点紧,不能使用 $O(\log |s|)$ 的Hash+二分。
考虑后缀数组,可以 $O(1)$ 查询。
发现需要查询区间的乘积,然而这是小数,由于精度的原因不能使用前缀积。
两种方法:
- 线段树,应该过不了。
- 猫树。
- 先取对数然后再取指数,使用前缀和。
时间复杂度 $O(n(\log n+30))$。
代码
这里写的是猫树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=8.4e5+5;
const int K=21;
int l2[N];
inline void init(int n)
{
l2[1]=0;
fo(i,2,n) l2[i]=l2[i>>1]+1;
}
namespace SuffixArray{
int base[N],t[N<<1];
int height[N<<1],sa[N<<1],rk[N<<1],f[N][K],len;
inline bool cmp(int x,int y,int k)
{
return t[x]==t[y]&&t[x+k]==t[y+k];
}
inline void rsort(int n,int m)
{
fo(i,0,m) base[i]=0;
fo(i,1,n) base[rk[t[i]]]++;
fo(i,1,m) base[i]+=base[i-1];
fd(i,n,1) sa[base[rk[t[i]]]--]=t[i];
}
inline void SA(int *a,int n,int m)
{
len=n; a[n+1]=m+1;
fo(i,1,n) t[i]=i,rk[i]=a[i];
rsort(n,m);
for(int w=1,p=0;p<n;w<<=1)
{
p=0;
fo(i,n-w+1,n) t[++p]=i;
fo(i,1,n) if(sa[i]>w) t[++p]=sa[i]-w;
rsort(n,p);
fo(i,1,n) t[i]=rk[i];
rk[sa[1]]=p=1;
fo(i,2,n) rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
}
for(int i=1,j,k=0;i<=n;height[rk[i++]]=k)
for(j=sa[rk[i]-1],(k?(k--):0);a[i+k]==a[j+k];k++);
fo(i,1,n) f[i][0]=height[i];
fo(j,1,K-1)
fo(i,1,n)
{
f[i][j]=f[i][j-1];
if(i+(1<<j)-1<=n) f[i][j]=min(f[i][j],f[i+(1<<(j-1))][j-1]);
}
fo(i,0,n) t[i]=0;
}
inline int ask_sa(int x,int y)
{
x=rk[x]; y=rk[y];
if(x>y) swap(x,y);
x++;
int k=l2[y-x+1];
return min(f[x][k],f[y-(1<<k)+1][k]);
}
}
using SuffixArray::ask_sa;
int a[N],n,m;
int l[N],r[N];
db w[N][10];
namespace CatTree{
db a[N],s[K][N];
int len,pos[N];
void build(int u,int l,int r,int d)
{
if(l==r)
{
pos[l]=u; return;
}
int mid=(l+r)>>1;
s[d][mid]=a[mid]; s[d][mid+1]=a[mid+1];
fd(i,mid-1,l) s[d][i]=s[d][i+1]*a[i];
fo(i,mid+2,r) s[d][i]=s[d][i-1]*a[i];
build(u<<1,l,mid,d+1);
build(u<<1|1,mid+1,r,d+1);
}
inline void build(int *b,int n)
{
fo(i,1,n) a[i]=w[i][b[i]-l[i]];
len=1;
for(;len<n;len<<=1);
fo(i,n+1,len) a[i]=0;
build(1,1,len,1);
}
inline db ask(int x,int y)
{
if(x>y) return 1.;
if(x==y) return a[x];
int d=l2[pos[x]]-l2[pos[x]^pos[y]];
return s[d][x]*s[d][y];
}
}
using CatTree::ask;
int main()
{
init(8.4e5);
CASET
{
printf("Case #%d:\n",___);
n=read(); m=read();
int id;
fo(i,1,n)
{
l[i]=read(),r[i]=read();
id=0;
fo(j,0,r[i]-l[i])
{
w[i][j]=((db)read())*(1e-9);
if(w[i][id]<=w[i][j]) id=j;
}
a[i]=id+l[i];
}
a[n+1]=n+1;
fo(i,1,m) a[n+1+i]=read();
CatTree::build(a,n);
SuffixArray::SA(a,n+m+1,n+2);
int le,ri,len;
db ans=1;
fo(i,1,n-m+1)
{
ans=1;
le=i,ri=n+2;
for(;ri<=n+m+1&&ans>1e-10;)
{
len=ask_sa(le,ri);
ans*=ask(le,le+len-1);
le=le+len; ri=ri+len;
if(ri<=n+m+1)
{
if(l[le]<=a[ri]&&a[ri]<=r[le])
ans*=w[le][a[ri]-l[le]];
else
ans=0;
}
le++,ri++;
}
if(ans<=1e-10) ans=0;
printf("%.12lf\n",ans);
}
fo(i,1,n+m+1) a[i]=0;
}
return 0;
}
|
C
题意
问有多少个 $1\sim n$ 的排列,使得插入排序进行了 $k$ 轮以后,该排列的最长上升子序列至少为 $n-1$。
$n\le 50,k\le 50$。
题解
考虑前 $k$ 个位置是否形成一个 $1\sim k$ 的排列,若不是,则只有一个 $k+1\sim n$ 的数在位置 $1\sim k$ 内。
分两种情况讨论。
答案为 $k!(1+(n-k)\times (n-k-1)+k\times (n-k))=k!((n-k)\times (n-1)+1)$。
时间复杂度 $O(k)$,当然可以优化到 $O(\frac{\sqrt{k}}{\log k})$,不过没有必要。
D
题意
给定一棵带边权的树,$m$ 次询问,问给每条边边权加了 $k$ 后,树的直径长度。
$n,m\le 2\times 10^5$
题解
这题是CF1019E的弱化版。
考虑1019E的题目:每条边有边权 $a,b$,每次询问边权变为 $ak+b$ 后的直径。
和树的路径有关,考虑分治。
但点分治的不好之处在于分成了大于等于 $2$ 的分治结构,在处理最值等问题而不是方案数的时候会有点复杂。
考虑边分治,为了使得两点间的信息不变,可以这样重构原树:
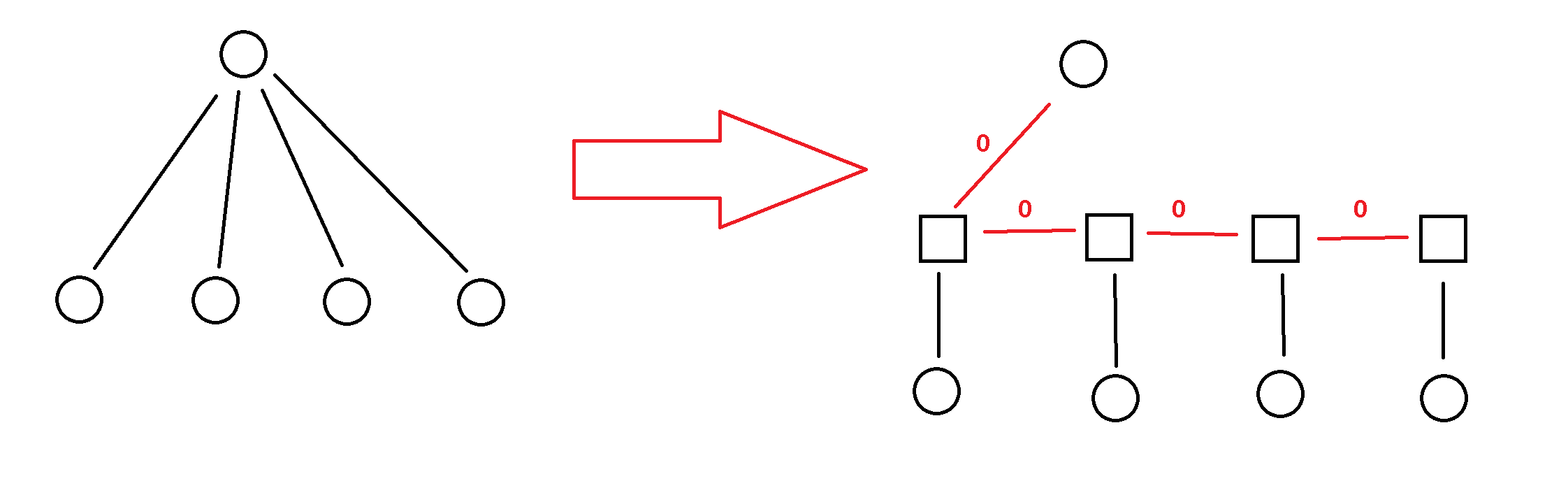
(之前的边分治重构写得太丑了)
边分治后,假设已经统计出所有的可能的答案,形如 $(a,b)$ 的形式。
我们需要使 $ak+b$ 最大,那就是用一个斜率为 $-k$ 的直线去切这些点集,使得纵截距最大。
于是建一个上凸包即可。
下面考虑,经过边分治后变成了两个子结构,统计经过所选分治中心的 $(a,b)$:
相当于有两个集合,每个集合上为 $(a,b)$,需要算出 $(a,b)+(c,d)$ 的上凸包。
显然就是闵科夫斯基和。
注意归并排序的时候需要注意不能越界!!!(已经死过很多遍了…,记得写全条件)
时间复杂度 $O(n\log ^2n+m\log n\log \log n)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=400010;
int n,m,cnt;
vector<pair<int,int> > adj[N];
int ne[N<<1],ver[N<<1],a[N<<1],b[N<<1],head[N],tot;
bool vis[N<<1];
inline void add(int x,int y,int _a,int _b)
{
ver[++tot]=y; a[tot]=_a; b[tot]=_b; ne[tot]=head[x]; head[x]=tot; vis[tot]=0;
ver[++tot]=x; a[tot]=_a; b[tot]=_b; ne[tot]=head[y]; head[y]=tot; vis[tot]=0;
}
void re_dfs(int u,int pre)
{
vector<pair<int,int> > vec;
vec.clear();
for(auto v:adj[u])
if(v.fi!=pre)
{
re_dfs(v.fi,u);
vec.pb(v);
}
if(vec.size()==1)
{
add(u,vec[0].fi,1,vec[0].se);
return;
}
int las=u;
for(auto v:vec)
{
++cnt;
add(las,cnt,0,0);
add(cnt,v.fi,1,v.se);
las=cnt;
}
}
inline void rebuild(int &n)
{
tot=1;
cnt=n;
re_dfs(1,0);
n=cnt;
}
int u1,u2,now,mi,id;
int siz[N];
void dfs(int u,int pre)
{
siz[u]=1;
for(int i=head[u],v;i;i=ne[i])
if(!vis[i]&&(v=ver[i])!=pre)
{
dfs(v,u);
siz[u]+=siz[v];
if(max(siz[v],now-siz[v])<mi)
{
mi=max(siz[v],now-siz[v]);
u1=v; u2=u; id=i;
}
}
}
struct P{
ll a,b;
friend inline bool operator<(const P &A,const P &B)
{
if(A.a==B.a) return A.b<B.b;
return A.a<B.a;
}
friend inline P operator-(const P &A,const P &B)
{
return (P){A.a-B.a,A.b-B.b};
}
friend inline P operator+(const P &A,const P &B)
{
return (P){A.a+B.a,A.b+B.b};
}
friend inline bool operator==(const P &A,const P &B)
{
return A.a==B.a&&A.b==B.b;
}
};
inline ll cross(P A,P B)
{
return A.a*B.b-B.a*A.b;
}
vector<P> v1,v2,s;
inline void build(vector<P> &A)
{
static vector<P> B;
B.clear();
sort(all(A));
A.resize(unique(all(A))-A.begin());
for(auto x:A)
{
while(B.size()>=2&&cross(B[B.size()-1]-B[B.size()-2],x-B[B.size()-2])>0) B.pop_back();
B.pb(x);
}
A=B;
}
void print(vector<P> &A)
{
DEBUG(A.size());
for(auto x:A) cerr<<" "<<x.a<<' '<<x.b<<endl;
}
inline void merge(vector<P> &A,vector<P> &B)
{
build(A); build(B);
int i=0,j=0;
for(;i<A.size()-1||j<B.size()-1;)
{
s.pb((P){A[i]+B[j]});
if(j<B.size()-1&&(i==A.size()-1||cross(B[j+1]-B[j],A[i+1]-A[i])<0))
j++;
else
i++;
}
s.pb(A[i]+B[j]);
}
void dfs2(int u,int pre,ll aa,ll bb,vector<P> &V)
{
V.pb((P){aa,bb});
for(int i=head[u],v;i;i=ne[i])
if(!vis[i]&&(v=ver[i])!=pre)
dfs2(v,u,aa+a[i],bb+b[i],V);
}
void divide(int u,int si)
{
if(si<=1){return;}
now=si; u1=u2=0; mi=1e9;
dfs(u,0);
int s1=siz[u1],s2=si-siz[u1],u3=u2;
vis[id]=vis[id^1]=1;
v1.clear(); v2.clear();
dfs2(u1,u2,a[id],b[id],v1);
dfs2(u2,u1,0,0,v2);
merge(v1,v2);
divide(u1,s1);
divide(u3,s2);
}
inline bool check(int x,int y,ll k)
{
return s[x].b-s[x].a*k>s[y].b-s[y].a*k;
}
int main()
{
CASET
{
printf("Case #%d:\n",___);
n=read(); m=read();
s.clear();
int x,y,z;
fo(i,2,n)
{
x=read(); y=read(); z=read();
adj[x].pb(mp(y,z)); adj[y].pb(mp(x,z));
}
rebuild(n);
divide(1,n);
build(s);
int l,r,mid;
ll k;
fo(i,1,m)
{
k=-read();
l=1,r=s.size()-1;
for(;l<=r;)
{
mid=(l+r)>>1;
if(check(mid-1,mid,k)) r=mid-1;
else l=mid+1;
}
l--;
printf("%lld\n",s[l].b-s[l].a*k);
}
fo(i,1,n) adj[i].clear(),head[i]=0;
}
return 0;
}
|
E
题意
给定二维平面上 $n$ 个点的坐标及颜色,有以下三种操作:
- 修改一点的坐标。
- 修改一点的颜色。
- 询问在编号为 $[l,r]$ 的点中,选择两个颜色不同的点的曼哈顿距离的最大值。
$n,m\le 10^5,\sum n,\sum m\le 5\times 10^5$。
题解
先考虑所有颜色相同,如何求一堆点的曼哈顿距离的最大值。
考虑经典的套路,将 $(x,y)$ 变为 $(x+y,x-y)$,转换为切比雪夫距离,即 $\max{|x_1-x_2|,|y_1-y_2|}$。
这样做的好处是将曼哈顿距离的二维转换成一维。
那么一堆颜色相同的点的距离的就是 $\max{|x_{max}-x_{min}|,|y_{max}-y_{min}|}$。
加入了颜色不相同的限制也十分无聊,记录最值,最值颜色,不同于最值颜色的次值即可。
时间复杂度 $O(n+m\log n)$,有大概12的常数。
F
这题的思路有点妙~
题意
给定一个有向无环图,点权,对于任意点均满足后继点的点权比该点小。
从某个点出发,选择三条长度至少为 $1$ 的,互不相同的,点权单调下降的路径,其价值为这三条路径的终点的权值之和。
对于每个 $k$,问有多少个由三条路径形成的集合,使得价值为 $k$。
$T\le 5,n\le 10000,m\le 30000,w\le 400$。
时限 6s。
题解
三条路径互不相同,可以容斥做。
考虑DP,设生成函数 $F_{i,j}$ 表示从 $i$ 出发,经过的所有点 $v$ 的 $x^{value_v\times j}$ 之和。
看起来答案就是 $[x^k]\frac{\sum_{i=1}^nF_{i,1}^3}{6}$。
但是,有两条路径重复,三条路径都重复的情况会被统计到,需要减去。
算一下容斥系数,发现答案就是 $[x^k]\frac{\sum F_{i,1}^3-3\sum F_{i,2}F_{i,1}+2\sum F_{i,3}}{6}$。
直接爆算,用拆系数FFT暴力,时间复杂度 $O(Tmw\log w)$,常数还巨大,显然过不了。
考虑最终的这个多项式,是一个 $3w$ 次的多项式。次数较小,考虑插值。
将 $0\sim 3w$ 代进多项式的 $x$ 中进行计算,然后再拉格朗日插值,算出最终多项式的系数就可以了。
时间复杂度 $O(T(n+m+w)w)$。
拉格朗日插值时可以将 $\prod_{i=0}^{3w}(x-i)$ 的系数暴力算出,然后暴力除一个 $(x-i)$。
由于有个地方用了快速幂,导致程序是卡着时间过的。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const ll mod=1e9+7;
inline ll Add(ll x,ll y){x+=y; return (x<mod)?x:x-mod;}
inline ll Dec(ll x,ll y){x-=y; return (x<0)?x+mod:x;}
inline ll Mul(ll x,ll y){return x*y%mod;}
inline ll Pow(ll x,ll y)
{
y%=(mod-1);ll ans=1;for(;y;y>>=1,x=x*x%mod)if(y&1) ans=ans*x%mod;
return ans;
}
const int N=10005;
const int W=1203;
vector<int> adj[N];
int value[N],deg[N],id[N];
queue<int> q;
int n,m,w,cnt;
ll f[N][3][W],a[W],g[W],h[W],ans[W],inv[W],pw[W][N];
int main()
{
ff(i,1,W) inv[i]=Pow(i,mod-2);
CASET
{
n=read(); m=read(); w=read()*3;
fo(i,1,n) value[i]=read(),adj[i].clear();
int x,y;
fo(i,1,m)
{
x=read(); y=read();
adj[x].pb(y);
deg[y]++;
}
fo(i,1,n) if(!deg[i]) q.push(i);
cnt=0;
for(int u;!q.empty();)
{
u=q.front(); q.pop();
id[++cnt]=u;
for(auto v:adj[u])
{
deg[v]--;
if(!deg[v]) q.push(v);
}
}
int u;
fo(i,0,w) fo(j,1,n) pw[i][j]=Pow(i,value[j]);
fo(i,0,w+1) a[i]=g[i]=ans[i]=0;
fd(t,n,1)
{
u=id[t];
fo(i,1,3)
fo(j,0,w)
f[u][i-1][j]=Pow(pw[j][u],i);
for(auto v:adj[u])
fo(i,0,2)
fo(j,0,w)
f[u][i][j]=Add(f[u][i][j],f[v][i][j]);
ll sum;
fo(j,0,w)
{
sum=(f[u][0][j]*f[u][0][j]%mod*f[u][0][j]-3ll*f[u][0][j]*f[u][1][j]+2ll*f[u][2][j]);
a[j]=Add(a[j],(sum%mod+mod)%mod);
}
}
g[0]=1;
fo(i,0,w)
{
fo(j,0,i+1) h[j]=0;
fo(j,0,i)
h[j]=Add(h[j],(mod-i)*g[j]%mod),
h[j+1]=Add(h[j+1],g[j]);
fo(j,0,i+1) g[j]=h[j];
}
fo(i,0,w)
{
fo(j,0,w+1) h[j]=g[j];
fd(j,w,1) h[j]=Add(h[j],h[j+1]*i%mod);
fo(j,0,i-1) a[i]=a[i]*inv[i-j]%mod;
fo(j,i+1,w) a[i]=a[i]*(mod-inv[j-i])%mod;
fo(j,0,w) ans[j]=Add(ans[j],h[j+1]*a[i]%mod);
}
printf("Case #%d:",___);
fo(i,1,w) printf(" %lld",inv[6]*ans[i]%mod);
printf("\n");
}
return 0;
}
|
G
题意
每次对一个二维平面有四种操作:
- 加入一个点 $(x,y)$ ,权值为 $w$。
- 删除一个点。
- 将与 $(x,y)$ 欧几里得距离为 $\sqrt{k}$ 的存在的点的权值加上 $w$。
- 求与 $(x,y)$ 欧几里得距离为 $\sqrt{k}$ 的存在的点的权值之和。
$m\le 2\times 10^5,k\le 10^7$。
时限12s。
题解
与一个点欧几里得距离为 $\sqrt{k}$ 的点很少,最多大概是 $48\times 4$ 。
用vector记录,然后暴力。
H
不会。。。
I
之前做过的一道FWT。
J
签到题。定义一些变量或者数组,求用去的MB数向上取整的结果。
K
题意
给定 $T\le 1000$ 组数据,每组数据三个数 $n,m,k$,求 $n$ 个人的约瑟夫环游戏(每数到第 $k$ 个人,该人出局)中第 $m$ 个出局的人的编号。
$\sum \min{m,k}\le 2\times 10^6$
题解
先来看看最经典的约瑟夫环问题如何解决:
求 $n$ 个人的约瑟夫环游戏(每数到第 $k$ 个人,该人出局)中最后一个出局的人的编号。
设 $f(n)$ 表示有 $n$ 个人时最后出局的编号。考虑第一次走了 $k$ 步后,就变成了 $n-1$ 的子问题,因此有:
$f(n)=(k+f(n-1))\bmod n,f(1)=0$。
那么,类似于上面的定义,设 $f(n,m)$ 表示 $n$ 个人时,第 $m$ 个出局的编号。
类似地,有:
$f(n,m)=(k+f(n-1,m-1))\bmod n,f(n,1)=(k-1)\bmod n$。
于是,如果 $m\le 2\times 10^6$ ,那么直接根据 $f$ 的定义,就可以求出来了。
对于 $k\le 2\times 10^6$,可以发现,$f(n,m)$ 的定义中 $k+f(n-1,m-1)$ 超过 $n$ 的次数大概是 $O(k)$ 次的,那么假设计算到 $f(n’,m’)$,设加了 $t$ 次后,依然小于那时候的 $n$,则有:
$f(n’,m’)+kt<n’+t$;
解得:$t<\frac{n’-f(n’,m’)}{k-1}$。
于是,特判掉 $k=1$,然后就可以计算了。
可以不分类,直接写成第二种形式就可以了。
时间复杂度 $O(\sum\min{m,k})$。
M
题意
$n$ 个多项式 $F_i(x)=(1+x^{b_i}+x^{2b_i}+\cdots + x^{a_ib_i})$,
$m$ 次询问 $\prod_{i=l}^rF_i(x)$ 的前 $c$ 项和。
强制在线。
$n,m\le 10000,a_i,b_i,c\le 1000$。
题解
$F_i(x)=(1+x^{b_i}+x^{2b_i}+\cdots + x^{a_ib_i})=\frac{1-x^{(a_i+1)b_i}}{1-x}$。
那么 $F_{i}(x)^{-1}=\frac{1-x}{1-x^{(a_i+1)b_i}}$。
于是 $\prod_{i=l}^rF_i(x)=\frac{\prod_{i=1}^rF_i(x)}{\prod_{i=1}^{l-1}F_i(x)}$。
于是只需计算 $F_i(x)$ 的前缀积以及 $F_i(x)$ 的逆的前缀积。
于是变成两种操作:
对一多项式乘上 $(1-x^w)$。
暴力即可。
对一多项式除去 $(1-x^w)$。
就是相当于 $1$ 的操作倒过来,也可以 $O(c)$ 去做。
算出前缀积后,要算两个前缀积的乘积的前 $c$ 项,这个也可以 $O(c)$ 做。
时间复杂度 $O((n+m)c)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const ll mod=1e9+7;
inline ll Add(ll x,ll y){x+=y; return (x<mod)?x:x-mod;}
inline void ADD(ll &x,ll y){x+=y; (x<mod)?0:x-=mod;}
inline ll Dec(ll x,ll y){x-=y; return (x<0)?x+mod:x;}
inline ll Mul(ll x,ll y){return x*y%mod;}
inline ll Pow(ll x,ll y)
{
y%=(mod-1);ll ans=1;for(;y;y>>=1,x=x*x%mod)if(y&1) ans=ans*x%mod;
return ans;
}
const int N=1005;
const int M=10005;
ll f[M][N],g[M][N],tmp[N];
int n,m,c;
int a[M],b[M];
int main()
{
CASET
{
n=read(); m=read(); c=1000;
fo(i,1,c) f[0][i]=g[0][i]=0;
f[0][0]=g[0][0]=1;
fo(i,1,n)
{
a[i]=read(); b[i]=read();
fo(j,0,c) tmp[j]=0;
fo(j,0,c)
{
if(j+(a[i]+1)*b[i]<=c)
tmp[j+(1+a[i])*b[i]]=Dec(tmp[j+(1+a[i])*b[i]],f[i-1][j]);
ADD(tmp[j],f[i-1][j]);
}
fo(j,0,c)
{
if(j>=b[i]) ADD(tmp[j],tmp[j-b[i]]);
f[i][j]=tmp[j];
}
fo(j,0,c) tmp[j]=0;
fd(j,c,0)
{
if(j+b[i]<=c) tmp[j+b[i]]=Dec(tmp[j+b[i]],g[i-1][j]);
tmp[j]=Add(tmp[j],g[i-1][j]);
}
int w=(a[i]+1)*b[i];
fo(j,0,c-w) ADD(tmp[j+w],tmp[j]);
fo(j,0,c) g[i][j]=tmp[j],tmp[j]=0;
}
ll ans=0,s,s2;
printf("Case #%d:\n",___);
for(int l,r;m--;)
{
l=(read()+ans)%n+1,r=(read()+ans)%n+1; c=read();
if(l>r) swap(l,r);
l--;
s=s2=0;
fo(i,0,c) ADD(s2,f[r][i]);
fo(i,0,c)
{
ADD(s,s2*g[l][i]%mod);
s2=Dec(s2,f[r][c-i]);
}
ans=s%mod;
printf("%lld\n",ans);
}
}
return 0;
}
|
