Codeforces Global Round 1[CF1110]

发表于 分类于

题目链接

A,B都没什么好说的。

C. Meaningless Operations

题意：多次询问，求 $f(a)=\max_{0 < b < a}\gcd(a\oplus b,a & b)$。

先用二进制表示 $a$，显然有 $\gcd(a\oplus b,a& b)\leq a\oplus b$，设 $a$ 的最高二进制位为 $x$，则 $a\oplus b\leq 2^{x+1}-1$。

可以发现，当 $a\not = 2^{x+1}-1$ 时，$a\oplus b$ 能取到最大值。此时有：$a+b=2^{x+1}-1$，则 $a& b=0$，因此 $\gcd$ 也能取到最大值。

那么当 $a=2^{x+1}-1$ 时，$a\oplus b=a-b,a& b=b$，则 $\gcd(a\oplus b,a& b)=\gcd(a-b,b)=\gcd(a,b)$，找到 $a$ 的最大不是本身的因子即可。

D. Jongmah

如果出现了三个 $(x-1,x,x+1)$，则可以用 $(x-1,x-1,x-1),(x,x,x),(x+1,x+1,x+1)$ 代替。

也就是一种合法的方案一定能转换成每种 $(x-1,x,x+1)$ 不超过 $2$ 个的形式。

设 $f_{i,j,k}$ 表示考虑到第 $i$ 位，$(i-1,i,i+1)$ 有 $j$ 个，$(i,i+1,i+2)$ 有 $k$ 个的最大值，然后DP即可。

1
2
3
4
5
6
7
8
9
memset(f,-1,sizeof(f));
f[0][0][0]=0;
fo(i,1,m)
	fo(j,0,2)
		fo(k,0,2)
			fo(l,0,2)
				if(f[i-1][k][l]!=-1&&j+k+l<=a[i])
					f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+l+(a[i]-j-k-l)/3);
printf("%lld",f[m][0][0]);

E. Magic Stones

题意：给一个序列 $c$，每次选一个 $i\in[2,n-1]$，将 $c_i$ 变成 $c_{i-1}+c_{i+1}-c_i$，问是否能将 $c$ 变成序列 $t$。

这种题通常都是差分或者前缀和就搞出来了。

首先必须要有 $c_1=t_1,c_n=t_n$。

我们进行差分，设 $a_i=c_{i}-c_{i-1}$，发现上述的操作实际上是在交换两个相邻的 $a_i$。题意转换成你可以交换任意相邻的数字，使得最后序列等于某个序列，排个序就没了。

F. Nearest Leaf

题意：

给定一棵带边权树，满足按照节点编号从小到大的顺序dfs得到的dfs序 $dfn_i=i$。

多次询问，可离线，求 $[l,r]$ 中所有的叶子结点点 $v$ 最近的距离。

$n,q\leq 5\times 10^5$

那就离线吧，把询问挂到树上，然后在dfs时处理询问。

假设你从 $u$ 开始经过了一条边 $(u,v,w)$，$w$ 表示权值，那么有些叶子结点的距离就 $+w$，有些就 $-w$，并且 dfs 序都是 $O(1)$ 段区间。由题目的性质知道对于的节点编号也是 $O(1)$ 段区间。

那么用线段树，把非叶子结点的距离设为 $+\infty$ ，然后随便打打标记就好了。

时间复杂度 $O(n\log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
	int x=0; char ch=getchar(); bool f=0;
	for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
	return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=5e5+5;
const ll inf=1ll<<60;
namespace SGT{
	#define lc (u<<1)
	#define rc (u<<1|1)
	#define ls lc,l,mid
	#define rs rc,mid+1,r
	ll mx[N<<2],tag[N<<2];
	inline void pushtag(int u,ll x)
	{
		mx[u]+=x; tag[u]+=x;
	}
	inline void pushdown(int u)
	{
		if(!tag[u]) return;
		pushtag(lc,tag[u]);
		pushtag(rc,tag[u]);
		tag[u]=0;
	}
	inline void pushup(int u)
	{
		mx[u]=min(mx[lc],mx[rc]);
	}
	void add(int u,int l,int r,int L,int R,ll v)
	{
		if(L<=l&&r<=R) return pushtag(u,v);
		int mid=l+r>>1;
		pushdown(u);
		if(L<=mid) add(ls,L,R,v);
		if(mid<R)  add(rs,L,R,v);
		pushup(u);
	}
	ll ask(int u,int l,int r,int L,int R)
	{
		if(L<=l&&r<=R) return mx[u];
		pushdown(u);
		int mid=l+r>>1;
		ll ans=inf;
		if(L<=mid) ans=min(ans,ask(ls,L,R));
		if(mid<R)  ans=min(ans,ask(rs,L,R));
		return ans;
	}
	void ins(int u,int l,int r,int p,ll v)
	{
		if(l==r) return (void)(mx[u]=v);
		int mid=l+r>>1;
		(p<=mid)?ins(ls,p,v):ins(rs,p,v);
		pushup(u);
	}
}

struct query{
	int l,r,id;
};
vector<query> q[N];
vector<int> leaf;
int n,m,fa[N];
ll ans[N],now;
int ver[N],val[N],ne[N],head[N],tot=1;
inline void add(int x,int y,int z)
{
	ver[++tot]=y; val[tot]=z; ne[tot]=head[x]; head[x]=tot;
}
int le[N],ri[N];
void dfs(int u)
{
	for(auto x:q[u])
		ans[x.id]=SGT::ask(1,1,n,x.l,x.r)+now;
	for(int i=head[u],v;i;i=ne[i])
	{
		v=ver[i];
		now+=val[i];
		SGT::add(1,1,n,le[v],ri[v],-val[i]*2);
		dfs(v);
		now-=val[i];
		SGT::add(1,1,n,le[v],ri[v],val[i]*2);
	}
}
void pre(int u,ll now)
{
	le[u]=n+1,ri[u]=0;
	for(int i=head[u],v;i;i=ne[i])
	{
		v=ver[i];
		pre(v,now+val[i]);
		le[u]=min(le[u],le[v]);
		ri[u]=max(ri[u],ri[v]);
	}
	if(!head[u]) le[u]=ri[u]=u,SGT::ins(1,1,n,u,now);
	else SGT::ins(1,1,n,u,inf);
}
int main()
{
	n=read(); m=read();
	fo(i,2,n)
	{
		fa[i]=read();
		add(fa[i],i,read());
	}
	fo(i,1,n) if(!head[i]) leaf.pb(i);
	pre(1,0);
	int v,l,r;
	fo(i,1,m)
	{
		v=read(); l=read(); r=read();
		l=lower_bound(all(leaf),l)-leaf.begin();
		r=upper_bound(all(leaf),r)-leaf.begin()-1;
		if(l>r) continue;
		q[v].pb((query){leaf[l],leaf[r],i});
	}
	dfs(1);
	fo(i,1,m) printf("%lld\n",ans[i]);
	return 0;
}

G. Tree-Tac-Toe

我们假设先不考虑刚开始就是白色的点。

首先显然的是，黑色不可能赢，因为如果黑色有必胜策略的话，白色能先走它的这个必胜策略。

那么看什么时候白色能赢。

设点 $i$ 的度数为 $deg_i$。

第一种情况：显然有，若存在 $i$ ，使得 $deg_i\geq 4$ ，则白色必赢。

第二种情况：接下来考虑度数是 $3$ 的点，发现如果他所连的三个点中存在至少两个不是叶子结点，那么白色也必胜了。

第三种情况：排除了上面两种情况以后，剩下的只能是一条链，然后在链的第二个和倒数第二个的点上最多再挂一个点的形式。

如果这两个点上都没再挂一个点，那么最后只能是平局。

最后只剩下这种：

G1

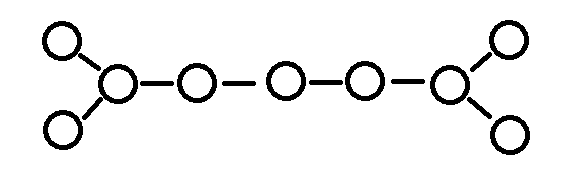
可以发现，当直径上点的长度是奇数的时候，白色必胜。

那么最后来考虑刚开始就有白色的情况。

它相当于你把这个点染成白色以后，必须要有一步黑色的操作，且这个黑色的操作不能影响到原来的点。

也就是必须设计一个东西，然后挂在这个被染成白色的点上面。

显然可以这样设计：

G2

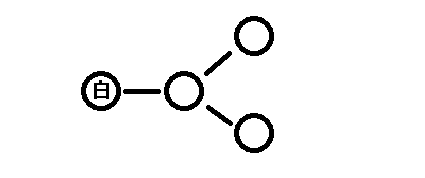
当你选了白点以后，如果黑色不选这个中间的点，那么下一步白色选它，黑色就输了。

那么这题就能做了。时间复杂度 $O(n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
	int x=0; char ch=getchar(); bool f=0;
	for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
	return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=2000010;
int n,ans,deg[N];
vector<int> adj[N],vec;
inline void add(int x,int y)
{
	adj[x].pb(y); deg[x]++;
	adj[y].pb(x); deg[y]++;
}
char s[N];
int main()
{
	CASET
	{
		n=read(); ans=0;
		fo(i,2,n) add(read(),read());
		scanf("%s",s+1);
		fo(i,1,n) if(s[i]=='W')
		{
			add(i,++n);
			++n; add(n-1,n);
			++n; add(n-2,n);
		}
		if(n<=4)
		{
			puts("Draw");
			fo(i,1,n) deg[i]=0,adj[i].clear();
			continue;
		}
		vec.clear();
		fo(i,1,n)
			if(deg[i]>=4) {ans=1; break;}
			else if(deg[i]==3)
			{
				int cnt=0;
				for(int v:adj[i]) if(deg[v]>=2) cnt++;
				if(cnt>=2) {ans=1; break;}
			}
			else if(deg[i]==1)
			{
				for(int v:adj[i]) vec.pb(v);
			}
		if(!ans)
		{
			sort(all(vec));
			vec.resize(unique(all(vec))-vec.begin());
			int u=vec[0],v=vec[1];
			if(deg[u]==3&&deg[v]==3&&(n&1)) ans=1;
		}
		puts(ans?"White":"Draw");
		fo(i,1,n) deg[i]=0,adj[i].clear();
	}
	return 0;
}

H. Modest Substrings

题意

求一个字典序最小的长度为 $n$ 的数字串，满足不含前导零的子串所表示的数字在 $[l,r]$ 内的子串数目最多。输出这个子串数目和字符串。

$1\leq l \leq r \leq 10^{800},n\leq 200$，时限 5s，空间 1G。

题解

如果 $r-l$ 比较小的话，我们就可以把所有在 $[l,r]$ 内的数字建出一个AC自动机，然后在上面跑DP就好了。

类似于数位DP，如果某个时刻你选的数字已经脱离限制了，那么以后随便填就都可满足了。比如 $l=227$，$r=403$，第一位选了 $2$，当第二位选了 $3$ 的时候，后面随便乱选都满足在 $[l,r]$ 里面了（对应在AC自动机上是一个满10叉树）。

我们找到哪些前缀会在选完前缀的最后一个数后脱离限制。发现最多有 $800\times 10 \times 2=16000$ 个这样的前缀，找这些前缀分类讨论一下即可找到。

要注意，脱离了限制不代表一定可以满足在 $[l,r]$ 内，这个前缀还需要加上一定个数的字符才能在 $[l,r]$ 内。

然后对这些前缀建立AC自动机，然后在AC机上进行DP。

设 $f_{i,j}$ 表示考虑到第 $i$ 位，当前在AC自动机的第 $j$ 个点上的最值。

考虑往后转移，设此时字符串是 $s$，你在后面填上一个字符 $c$，看这个此时这个字符 $c$ 的贡献。

这个贡献相当于枚举 $s+c$ 的后缀，看这个后缀是否脱离限制，且后面能给它加足够的点来完成。那么设 $h_{j,k}$ 表示节点 $j$ 的点的fail链的所有点中，当中有 $h_{j,k}$ 个前缀满足需要再加 $k$ 个字符才能在 $[l,r]$ 内。

那么这个DP就是：$f_{i+1,ne_{j,c}}=\max{f_{i,j}+\sum_{k\leq n-i-1}h_{ne_{j,c},k}}$。

$h$ 做个前缀和即可快速转移。

时间复杂度 $O(nm\Sigma)$，其中 $m$ 为 AC自动机点数，$\Sigma$ 为字符集大小。

输出方案倒退回去再正推贪心即可。

程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
const int N=16100;
int n,m;
int ne[N][10],fail[N],cnt,h[N][2003];
inline int get_next(int x,int k)
{
	if(!ne[x][k]) ne[x][k]=++cnt;
	return ne[x][k];
}
queue<int> q;
void getfail()
{
	fo(i,0,9) if(ne[0][i]) q.push(ne[0][i]);
	for(int u;!q.empty();)
	{
		u=q.front(); q.pop();
		fo(i,0,m) h[u][i]+=h[fail[u]][i];
		fo(i,0,9)
		{
			int v=ne[u][i];
			if(!v) ne[u][i]=ne[fail[u]][i];
			else fail[v]=ne[fail[u]][i],q.push(v);
		}
	}
}
int init()
{
	int n1,n2;
	static char s1[805],s2[805];
	scanf("%s%s",s1,s2);
	n1=strlen(s1); n2=strlen(s2);
	int u1=0,u2=0;
	if(n1==n2)
	{
		ff(i,0,n1)
		{
			if(u1==u2)
			{
				fo(j,s1[i]-'0'+1,s2[i]-'0'-1) h[get_next(u1,j)][n1-i-1]++;
			}
			else
			{
				fo(j,s1[i]-'0'+1,9) h[get_next(u1,j)][n1-i-1]++;
				fo(j,(!i)?1:0,s2[i]-'0'-1) h[get_next(u2,j)][n2-i-1]++;
			}
			u1=get_next(u1,s1[i]-'0');
			u2=get_next(u2,s2[i]-'0');
		}
		h[u1][0]++;
		if(u1^u2) h[u2][0]++;
	}
	else
	{
		ff(i,0,n1)
		{
			fo(j,s1[i]-'0'+1,9) h[get_next(u1,j)][n1-i-1]++;
			u1=get_next(u1,s1[i]-'0');
		}
		ff(i,0,n2)
		{
			fo(j,(!i)?1:0,s2[i]-'0'-1) h[get_next(u2,j)][n2-i-1]++;
			u2=get_next(u2,s2[i]-'0');
		}
		h[u1][0]++; h[u2][0]++;
		fo(i,n1+1,n2-1)
			fo(j,1,9)
				h[get_next(0,j)][i-1]++;
	}
	return n2-1;
}
int f[2005][N];
bool vis[2005][N];
void solve()
{
	getfail();
	scanf("%d",&n);
	fo(i,0,cnt) fo(j,1,n) h[i][j]+=h[i][j-1];
	memset(f,128,sizeof(f));
	f[0][0]=0;
	fo(i,1,n)
		fo(j,0,cnt)
			if(f[i-1][j]>=0)
				fo(k,0,9)
					f[i][ne[j][k]]=max(f[i][ne[j][k]],f[i-1][j]+h[ne[j][k]][n-i]);
	int mx=0;
	fo(i,0,cnt) mx=max(mx,f[n][i]);
	printf("%d\n",mx);
	fo(i,0,cnt) if(f[n][i]==mx) vis[n][i]=1;
	fd(i,n-1,0)
		fo(j,0,cnt)
			if(f[i][j]>=0)
				fo(k,0,9)
					if(vis[i+1][ne[j][k]]&&f[i][j]+h[ne[j][k]][n-i-1]==f[i+1][ne[j][k]])
						vis[i][j]=1;
	int u=0;
	fo(i,1,n)
		fo(k,0,9)
			if(vis[i][ne[u][k]]&&f[i-1][u]+h[ne[u][k]][n-i]==f[i][ne[u][k]])
			{
				putchar(k^48);
				u=ne[u][k];
				break;
			}
}

int main()
{
	m=init();
	solve();
	return 0;
}