题意
一棵树,求所有三个不同的点,两两距离相同的方案数。
$n\leq 5000$
加强版:$n\leq 10^5$
题解
两个点可以在 $\mbox {LCA }$处统计,尝试着三个点也在 $\mbox LCA$ 那里统计答案?
三个点两两距离相同,说明必定存在一个点,使得这个点到这三个点距离均为 $d$。
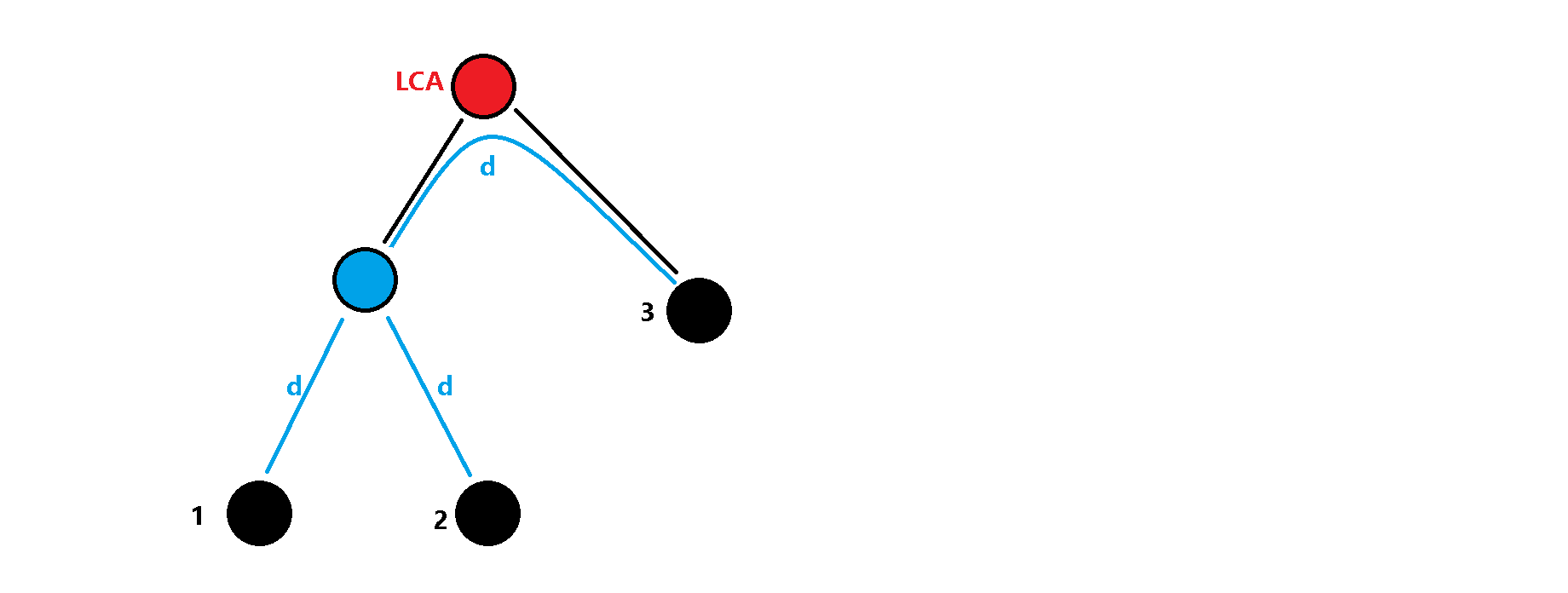
那么假设 $3$ 号点与 $\mbox {LCA}$ 的距离为 $j$,那么蓝点到 $\mbox{LCA}$ 的距离为 $d-j$。
因此可以设 $f_{i,j}$ 表示 $i$ 号点的子树中与 $i$ 距离为 $j$ 的点有多少个,设 $g_{i,j}$ 表示 $i$ 号点的子树中,某两个点到第三点的距离为 $d$,第三点到 $\mbox{LCA}$ 的距离为 $d-j$ 的方案数。
依次考虑每个儿子 $k$,DP方程大概长这样:
$$g_{i,j}=g’{i,j}+g{k,j+1}+f_{i,j}\times f_{k,j-1},\f_{i,j+1}=f’{i,j+1}+f{k,j}$$
统计答案:$g_{i,0}+\sum{f_{i,j}g_{k,j-1}}+\sum{f_{i,j-1}g_{k,j}}$
每一个 $k$ 的时间是 $O(len_k)$ 的。
显然可以 $O(n^2)$ DP一下。
既然复杂度跟 $len_k$ 相关,那么长链剖分一下就可以了。
重儿子的转移:$f_{son_i}=f_i+1,g_{son_i}=g_i-1$
预留够足够的空间就可以了。
时间复杂度 $O(n)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #define N 100010
int ver[N<<1],ne[N<<1],head[N],tot;
inline void add(int x,int y)
{
ver[++tot]=y; ne[tot]=head[x]; head[x]=tot;
ver[++tot]=x; ne[tot]=head[y]; head[y]=tot;
}
int n,len[N],son[N];
ll tmp[N<<2],*f[N],*g[N],*id=tmp,ans;
void dfs1(int u,int pre)
{
for(int i=head[u],v;i;i=ne[i])
if((v=ver[i])!=pre)
{
dfs1(v,u);
if(len[son[u]]<len[v]) son[u]=v;
}
len[u]=len[son[u]]+1;
}
void dfs2(int u,int pre)
{
if(son[u]) g[son[u]]=g[u]-1,f[son[u]]=f[u]+1,dfs2(son[u],u);
ans+=g[u][0]; f[u][0]=1;
for(int i=head[u],v;i;i=ne[i])
if((v=ver[i])!=pre&&ver[i]!=son[u])
{
f[v]=id; id+=len[v]<<1;
g[v]=id; id+=len[v]<<1;
dfs2(v,u);
fo(j,0,len[v]-1)
{
ans+=g[u][j+1]*f[v][j];
if(j!=len[v]-1) ans+=g[v][j+1]*f[u][j];
}
fo(j,0,len[v]-1)
{
g[u][j+1]+=f[u][j+1]*f[v][j];
if(j) g[u][j-1]+=g[v][j];
f[u][j+1]+=f[v][j];
}
}
}
int main()
{
n=read();
fo(i,2,n) add(read(),read());
dfs1(1,0);
f[1]=id; id+=len[1]<<1;
g[1]=id; id+=len[1]<<1;
dfs2(1,0); printf("%lld",ans);
return 0;
}
|
