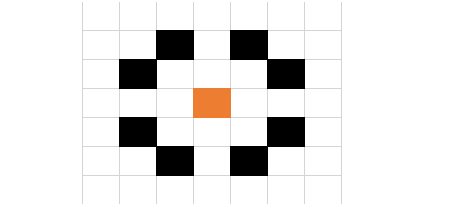链接
luogu
题解
就是一道裸构造题。
如图,对于橙色的格子,需要这 $8$ 个黑色格子的至少 $4$ 个。
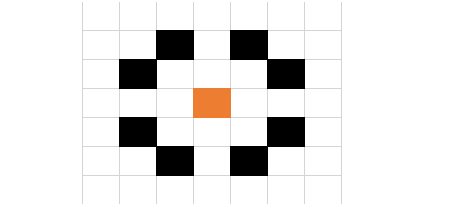
假设用下面的四个来搞出这个橙色的格子。
如果要搞出一行橙色,不难想到用两行即可。
如图所示:

红色的即为黑色两行通过上面的方法新搞出来的格子。
那么每次长度-4,设这黑色两行长度为 $m$,则一共大概有:$\frac{m\times \frac{m}{4}}{2}\times 2=\frac{m^2}{4}$。
显然有:$2n=m$,则一共约有 $\frac{n^2}{16}$ 个格子。还差一点。
既然两行搞不定,我们尝试来三行的。
显然这三行不需要全都涂满。经过乱搞发现这样就可以变成三行了:
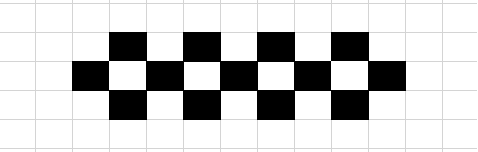
大概满足条件 $n=\frac{3}{2}m$,所以一共大概有 $\frac{m^2}{4}=\frac{n^2}{9}$ 个格子。
这样就可以做了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include <bits/stdc++.h>
using namespace std;
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
int n;
int main()
{
cin>>n;
if(n<=10)
{
fo(i,1,n) printf("%d %d\n",19260817+i,19890604+i);
return 0;
}
while(n%3!=1)
{
printf("%d %d\n",19260817+n,19890604+n);
n--;
}
fo(i,1,n/3) printf("3 %d\n",2*i);
fo(i,1,n/3+1) printf("2 %d\n",2*i-1);
fo(i,1,n/3) printf("1 %d\n",2*i);
return 0;
}
|