比赛链接
题目链接
没有队友,被爆踩了。最终因罚时排到了61名。
还是不能一次写对啊qwq。
D. Distinct Sub-palindromes
题意
问有多少个长度为 $n$ 的,由小写字母组成的字符串,使得本质不同的回文串个数最少。
输出个数对 $998244353$ 取模的结果。
题解
取模就是废的。
与本质不同的回文串个数相对应的是回文树上的节点个数减2。
打表得出前几个,26,676,17576,15600,15600,15600…
因此,时间复杂度 $O(1)$。
实际上考虑到 $n\leq 3$ 时答案就是 $26^n$。
当 $n>3$ 时,构造形如 $abcabca\cdots$ 这样的可以发现,本质不同的回文串只有 $3$ 个。
那么当出现字母的个数不为 $3$ 时也显然不可以的。
当出现字母为 $3$ 时不能出现形如 $aba$ 或者 $aa$ 这样的子串。
那么就只剩下构造出来的那种情况了。
此时答案就是 $26\times 25\times 24$。
程序
我想到了一个绝妙的写法,这里地方太小,写不下。
E. Fibonacci Sum
题意
给定 $n,c,k$,求 $\sum_{i=0}^n(F_{ic})^k$,其中 $F_i$ 为斐波那契数列第 $i$ 项。
对 $10^9+9$ 取模。
$T\leq 200,N,C\leq 10^{18},k\leq 10^5$。
题解
设 $a=\frac{\sqrt{5}+1}{2},b=\frac{1-\sqrt{5}}{2}$。
那么有:
$\sum_{i=0}^n(F_{ic})^k$
$=\sum_{i=0}^n(\frac{a^{ic}-b^{ic}}{\sqrt{5}})^k$
$=(\frac{1}{\sqrt{5}})^k\sum_{i=0}^n(a^{ic}-b^{ic})^k$
$=(\frac{1}{\sqrt{5}})^k\sum_{i=0}^n\sum_{j=0}^k\binom{k}{j}(a^{ic})^j(-b^{ic})^{k-j}$
$=(\frac{1}{\sqrt{5}})^k\sum_{j=0}^k\binom{k}{j}(-1)^{k-j}\sum_{i=0}^n(a^{cj}b^{c(k-j)})^i$
然后等比数列求和。
当时式子推错了一个地方调了好久好久,推式子时草稿一定要写好。
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const ll mod=1e9+9;
inline ll Add(ll x,ll y){x+=y; return (x<mod)?x:x-mod;}
inline ll Dec(ll x,ll y){x-=y; return (x<0)?x+mod:x;}
inline ll Mul(ll x,ll y){return x*y%mod;}
inline ll Pow(ll x,ll y)
{
y%=(mod-1);ll ans=1;for(;y;y>>=1,x=x*x%mod)if(y&1) ans=ans*x%mod;
return ans;
}
const int N=100010;
ll fac[N],inv[N];
void init(int n)
{
fac[0]=1; fo(i,1,n) fac[i]=fac[i-1]*i%mod;
inv[n]=Pow(fac[n],mod-2); fd(i,n,1) inv[i-1]=inv[i]*i%mod;
}
inline ll C(int n,int m)
{
if(n<0||m<0||n<m) return 0;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
const ll x=Pow(383008016,mod-2);
const ll a=691504013;
const ll b=308495997;
ll n,c,k;
int main()
{
init(100000);
ll _a,_b;
CASET
{
cin>>n>>c>>k;
c%=(mod-1);
ll ans=0,tmp,sum;
_a=Pow(a,c); _b=Pow(b,c);
fo(i,0,k)
{
tmp=Pow(_a,i)*Pow(_b,k-i)%mod;
if(tmp==1) sum=(n+1)%mod;
else sum=(Pow(tmp,n+1)-1+mod)%mod*Pow(tmp-1,mod-2)%mod;
if((k-i)%2==0)
ans=Add(ans,sum*C(k,i)%mod);
else
ans=Dec(ans,sum*C(k,i)%mod);
}
printf("%lld\n",ans*Pow(x,k)%mod);
}
return 0;
}
|
F. Finding a MEX
题意
给一个无向图,每个点上有点权。支持两种操作,一是修改某个点的点权,二是查询到某个点距离为 $1$ 的所有点的点权的Mex。
$T\leq 10,n,m,q\leq 10^5,a_i\leq 10^9$。
题解
这种套路都出烂了吧…
首先 $a_i\leq 10^9$ 是吓人的,实际上只需要有 $a_i\leq 10^5$,因为大过 $10^5$ 的数求Mex时不会碰到。
考试时就是因为忘记这里然后RE,导致调了十年。有时这些细节可以写在纸上或者程序旁。
然后数据分治,对于度数小于等于 $K$ 的点,我们暴力枚举旁边的点。
对于度数大于 $K$ 的点,最多有 $\frac{2m}{K}$ 个,然后对这些点相连的点的权值搞成一个桶,用分块或数据结构维护之。
空间和时间都大概是根号的。
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=100005;
const int Siz=1000;
vector<int> adj[N];
int deg[N],a[N],bel[N],cnt,siz[Siz+5][Siz+5];
int n,m,Sqr;
int flag[Siz+5][N];
bool bo[N];
inline void add(int x,int y)
{
adj[x].pb(y); adj[y].pb(x);
deg[x]++; deg[y]++;
}
int bl[N];
inline void add(int i,int y,int d)
{
flag[i][y]+=d;
siz[i][bl[y]]+=d;
}
int main()
{
for(int i=0,j=1;i<=100000;i+=Siz,j++)
{
int num=min(100000-i+1,Siz);
ff(k,0,num) bl[i+k]=j;
}
CASET
{
cnt=0;
n=read(); m=read(); Sqr=sqrt(2*m)+10;
fo(i,1,n)
{
a[i]=read();
if(a[i]>=100000) a[i]=100000;
}
fo(i,1,m) add(read(),read());
fo(i,1,n)
{
sort(all(adj[i]));
adj[i].resize(unique(all(adj[i]))-adj[i].begin());
if(deg[i]>=Sqr)
{
++cnt; bel[i]=cnt;
for(auto v:adj[i]) add(cnt,a[v],1);
}
}
fo(i,1,n)
sort(all(adj[i]),[&](const int &x,const int &y){return bel[x]>bel[y];});
for(int q=read(),u,x;q--;)
if(read()==1)
{
u=read(),x=read();
if(x>=100000) x=100000;
for(auto v:adj[u])
if(deg[v]>=Sqr)
{
add(bel[v],a[u],-1);
add(bel[v],x,1);
}
else break;
a[u]=x;
}
else
{
u=read(); int ans;
if(deg[u]<Sqr)
{
for(auto v:adj[u]) bo[a[v]]=1;
for(ans=0;bo[ans];ans++);
for(auto v:adj[u]) bo[a[v]]=0;
printf("%d\n",ans);
}
else
{
bool boo=0;
for(int i=0,j=1;i<=100000&&!boo;i+=Siz,j++)
{
int num=min(Siz,100000-i+1);
if(siz[bel[u]][j]==num) continue;
ff(k,0,num) if(!flag[bel[u]][i+k])
{
printf("%d\n",i+k); boo=1; break;
}
}
}
}
fo(i,1,n)
{
if(deg[i]>=Sqr)
for(auto v:adj[i]) add(bel[i],a[v],-1);
bel[i]=deg[i]=0;
adj[i].clear();
}
}
return 0;
}
|
I. Leading Robots
题意
一个数轴上 $n$ 个动点在往右走。
每个点初始位置为 $p_i$,加速度为 $a_i$,一开始速度为 $0$。问这样的点 $i$ 的个数:存在某个大于等于 $0$ 的实数时间 $t$,使得所有不是 $i$ 的点都严格在点 $i$ 左侧。
$n\leq 50000$。
题解
对于时间 $t$ 和两个点 $i,j$,点 $i$ 在点 $j$ 右侧的条件是:$p_i+\frac{a_it^2}{2}>p_j+\frac{a_jt^2}{2}$。
移项得:$p_i-p_j>(a_j-a_i)\frac{t^2}{2}$
因为 $t\geq 0$,所以 $\frac{t^2}{2}\geq 0$。
分类讨论一下,假设 $a_i>a_j$。
那么 $-\frac{p_i-p_j}{a_i-a_j}<\frac{t^2}{2}$。
按照 $a$ 的大小排序,将 $a$ 看成横坐标,$p$ 看成纵坐标。变成找到 $i$ 之前的点和点 $i$ 形成的直线的斜率的最小值。
这个比较容易,建一个上凸包即可。
$a_i<a_j$ 的情况同理。
那么对于 $\frac{t^2}{2}$ 找到了一个范围 $[L,R]$,满足 $L\le R,0\le R$ 即可。
注意判断相等的那些情况。
因为要排序,时间复杂度 $O(n\log n)$。
程序
考场代码,写得超级烂。。。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const int N=200010;
const db inf=1e18;
const db eps=1e-15;
struct node{
ll p,a; bool ok;
friend inline bool operator<(const node &A,const node &B)
{
if(A.a!=B.a) return A.a<B.a;
return A.p<B.p;
}
}q[N];
inline bool cmp(const node &A,const node &B)
{
return A.p<B.p;
}
inline ll Cross(int x,int y,int z)
{
return (q[y].a-q[x].a)*(q[z].p-q[x].p)-(q[z].a-q[x].a)*(q[y].p-q[x].p);
}
int n,top,st[N];
db L[N],R[N];
int main()
{
CASET
{
n=read();
fo(i,1,n) q[i].p=read(),q[i].a=read(),q[i].ok=1;
sort(q+1,q+n+1,cmp);
ll mx=0;
for(int i=1,j;i<=n;i=j)
{
mx=0;
for(j=i;j<=n&&q[i].p==q[j].p;j++) mx=max(mx,q[j].a);
fo(k,i,j-1) if(q[k].a!=mx) q[k].ok=0;
}
sort(q+1,q+n+1);
fo(i,1,n-1)
{
if(q[i+1].a==q[i].a&&q[i+1].p>=q[i].p) q[i].ok=0;
if(q[i+1].a==q[i].a&&q[i+1].p==q[i].p) q[i+1].ok=0;
}
st[top=1]=n; R[n]=inf;
fd(i,n-1,1)
if(q[i+1].p!=q[i].p||q[i+1].a!=q[i].a)
{
while(top>=2&&Cross(st[top-1],i,st[top])>0) top--;
if(q[i].ok) R[i]=-(db)(q[st[top]].p-q[i].p)/(q[st[top]].a-q[i].a);
st[++top]=i;
}
st[top=1]=1; L[1]=-1;
fo(i,2,n)
if(q[i-1].p!=q[i].p||q[i-1].a!=q[i].a)
{
while(top>=2&&Cross(st[top-1],st[top],i)>0) top--;
if(q[i].ok)
{
if(q[st[top]].a==q[i].a) L[i]=-1;
else L[i]=-(db)(q[st[top]].p-q[i].p)/(q[st[top]].a-q[i].a);
}
st[++top]=i;
}
fo(i,1,n) if(q[i].ok)
{
if(L[i]<R[i]&&R[i]>1e-12) q[i].ok=1;
else q[i].ok=0;
}
int ans=0;
fo(i,1,n) if(q[i].ok) ans++;
printf("%d\n",ans);
}
return 0;
}
|
K. Minimum Index
链接
L. Mow
题意
给一个 $n$ 个点的简单多边形,上面长满了草。
你需要在上面割草,有两种方式。
一种是使用手割,每割 $1$ 单位的草花费 $a$ 元;令一种是使用机器割,每割到 $1$ 单位的草花费 $b$ 元。
机器是一个半径为 $r$ 的圆,使用机器时,机器任意一个部位不能在多边形外面。
求割完所有草的最小花费。
$T\leq 100,n\leq 200$。
题解
分类讨论:若 $a\le b$,则显然直接用手割完即可。求出多边形面积,然后 $\times a$ 即可。下面只考虑 $a>b$ 的情况。
显然,我们需要机器割得越多越好。
那么机器能割多少呢?
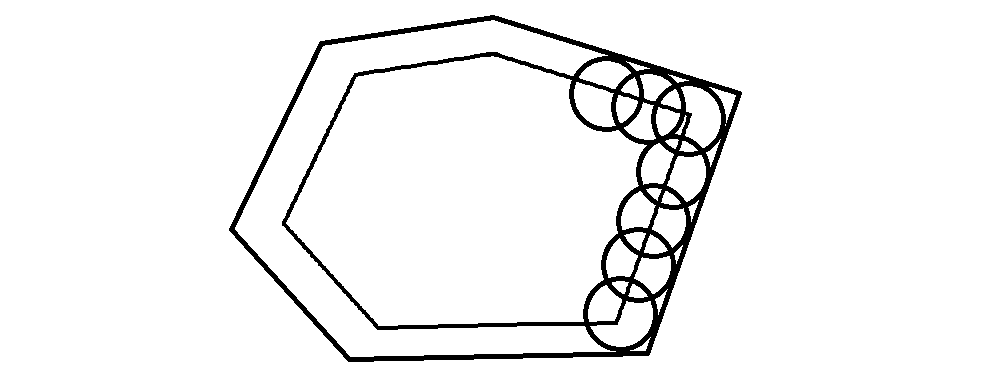
对于这个多边形而言,我们将多边形内部的边向里面移 $r$ 个单位,形成了一个新的多边形。设这个多边形的面积为 $s$,周长为 $c$,显然机器最多能割 $s+cr+\pi r^2$ 的面积。
现在只需要求出这个新多边形就好了。
首先我们将点逆时针排好。然后将 $n$ 条直线往里面移动。然后求移动完的直线的半平面交,即可求出新多边形。
需要注意这个新多边形可能是不存在的。
时间复杂度 $O(n)$。
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
| #include <bits/stdc++.h>
using namespace std;
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define fo(i,j,k) for(int i=(j),end_i=(k);i<=end_i;i++)
#define ff(i,j,k) for(int i=(j),end_i=(k);i< end_i;i++)
#define fd(i,j,k) for(int i=(j),end_i=(k);i>=end_i;i--)
#define DEBUG(x) cerr<<#x<<"="<<x<<endl
#define all(x) (x).begin(),(x).end()
#define cle(x) memset(x,0,sizeof(x))
#define lowbit(x) ((x)&-(x))
#define ll long long
#define ull unsigned ll
#define db double
#define lb long db
#define pb push_back
#define mp make_pair
#define fi first
#define se second
inline int read()
{
int x=0; char ch=getchar(); bool f=0;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);
return f?-x:x;
}
#define CASET fo(___,1,read())
const db eps=1e-9;
const db pi=acos(-1);
struct P{
db x,y;
inline db angle() {return atan2(y,x);}
inline db dis() {return sqrt(x*x+y*y);}
friend inline bool operator <(const P &A,const P &B)
{
if(fabs(A.x-B.x)<eps) return A.y<B.y;
return A.x<B.x;
}
friend inline P operator *(const P &A,const db &k)
{
return (P){A.x*k,A.y*k};
}
friend inline P operator -(const P &A,const P &B)
{
return (P){A.x-B.x,A.y-B.y};
}
friend inline P operator +(const P &A,const P &B)
{
return (P){B.x+A.x,B.y+A.y};
}
friend inline db operator *(const P &A,const P &B)
{
return A.x*B.y-B.x*A.y;
}
friend inline db operator ^(const P &A,const P &B)
{
return A.x*B.x+A.y*B.y;
}
};
struct L{
P x,y; db ang;
L(){}
L(P a,P b)
{
x=a; y=b-a; ang=y.angle();
}
inline db length()
{
return y.dis();
}
};
inline bool parallel(L A,L B)
{
return fabs(A.ang-B.ang)<eps;
}
inline P intersection(L A,L B)
{
P u=A.x-B.x;
return A.x+A.y*((B.y*u)/(A.y*B.y));
}
inline db Area(P *a,int n)
{
if(n<=2) return 0;
db sum=0;
fo(i,3,n) sum+=(a[i-1]-a[1])*(a[i]-a[1]);
return sum/2;
}
inline bool OnLeft(L A,P p)
{
return A.y*(p-A.x)>0;
}
inline bool OnRight(L A,P p)
{
return (p-A.x)*A.y>0;
}
inline bool operator<(const L &A,const L &B)
{
if(fabs(A.ang-B.ang)<eps) OnLeft(A,B.x);
return A.ang<B.ang;
}
const int N=2005;
P a[N],qp[N],p[N];
L ql[N];
db r;
inline db solve(L *l,int n)
{
sort(l+1,l+n+1);
int L=1,R=0;
ql[++R]=l[1];
fo(i,2,n)
{
for(;L<R&&OnRight(l[i],qp[R-1]);R--);
for(;L<R&&OnRight(l[i],qp[L]);L++);
ql[++R]=l[i];
if(fabs(ql[R].y*ql[R-1].y)<eps)
{
R--;;
if(OnLeft(ql[R],l[i].x)) ql[R]=l[i];
}
if(L<R) qp[R-1]=intersection(ql[R],ql[R-1]);
}
for(;L<R&&OnRight(ql[L],qp[R-1]);R--);
qp[R]=intersection(ql[R],ql[L]);
db c=0,s=0;
int m=0;
fo(i,L,R) a[++m]=qp[i];
if(m<=2) return 0;
s=Area(a,m);
fo(i,1,m) c+=(a[i%m+1]-a[i]).dis();
return c*r+pi*r*r+s;
}
L l[N];
int n;
int main()
{
db a,b;
db PolygonArea,MachineArea;
CASET
{
n=read(); r=read();
a=read(); b=read();
fo(i,1,n) p[i].x=read(),p[i].y=read();
PolygonArea=Area(p,n);
if(PolygonArea<0)
{
PolygonArea=-PolygonArea;
reverse(p+1,p+n+1);
}
if(a<b)
{
printf("%.12lf\n",PolygonArea*a);
continue;
}
fo(i,1,n)
{
P d=p[i%n+1]-p[i];
swap(d.x,d.y);
d.x=-d.x;
d=d*(r/d.dis());
l[i]=L(p[i]+d,p[i%n+1]+d);
}
MachineArea=solve(l,n);
printf("%.12lf\n",min(PolygonArea*a,(PolygonArea-MachineArea)*a+MachineArea*b));
}
return 0;
}
|
